观前提示，作者不是光学相关的专业人士，也不是以严谨闻名的数学家，因此内容中可能会存在些许（大量）不够严谨的地方，请忽略，但是，出现错误的地方还请指出，作者一定会进行改正，谢谢。

几何光学解释不了的东西

我们上初中的时候，有一个经典的关于凸透镜成像的问题，就是如果我们遮挡住了一步分的凸透镜，会不会影响成像。老师说的很简单（要不简单就得讲到高考了），图像会变暗，但是不会影响凸透镜成像。图像变暗很简单，入射的光像变少了，所以焦点的能量变小了（准确说是功率），所以图像当然变暗了。但是就没有其他影响了吗？从几何光学的角度来看的话，好像啥也看不出来。它就是遮住了光，其他光还是能正常成像。

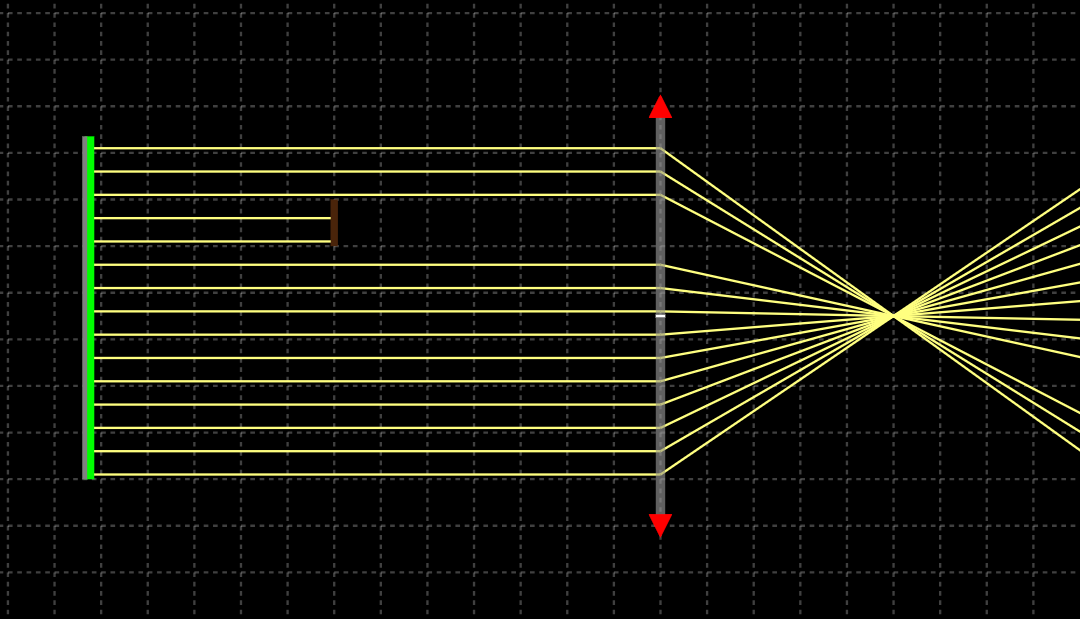
但是当我们深入天文望远镜的时候，总是会有一种说法，叫折射镜锐度高，反射式望远镜和折返式望远镜的锐度会差一些，而且是遮挡比越大，图像越糊，这是什么情况。

而且这也不能解释为什么在用鱼骨板对焦的时候会出现3条光线的问题——我只是遮住了一部分光线而已，为什么会对星点产生这种影响。

信息光学是什么

在深入研究这个问题之前，我们需要补一点小小的知识点。

一些前置的小（啸）知识

首先我们来看看一个完美的透镜会遇到的问题，衍射。衍射基本上决定了一个望远镜的分辨力极限，比如我们在查望远镜参数的时候经常会看到的多少角秒，就是对应的这个口径的分辨力极限。例如一个RC8,它的口径取203mm，那么根据经典的不能再经典的艾里斑角半径，有：

\(sin\theta =1.22\frac{\lambda}{d} \)

我们把RC8的参数带入进去，并且假设我们观测的波长是550nm,就能算出系统角分辨力大约是0.68度。

显然我们没有考虑到RC8相对巨大的遮挡比。

其实几何光学没能解决的问题，基本上都是遇到了类似衍射这种波动光学的问题，一想到波动光学的问题，就会有一大堆的波与波之间的叠加之类的种种复杂的公式和各种光程差之类的东西，看到就让人头大，我们先把它们放在一边，先来看看一个看似完全不相关的东西，一个随着时间变换的电压（或者别的什么）信号U(t),假设它长这样

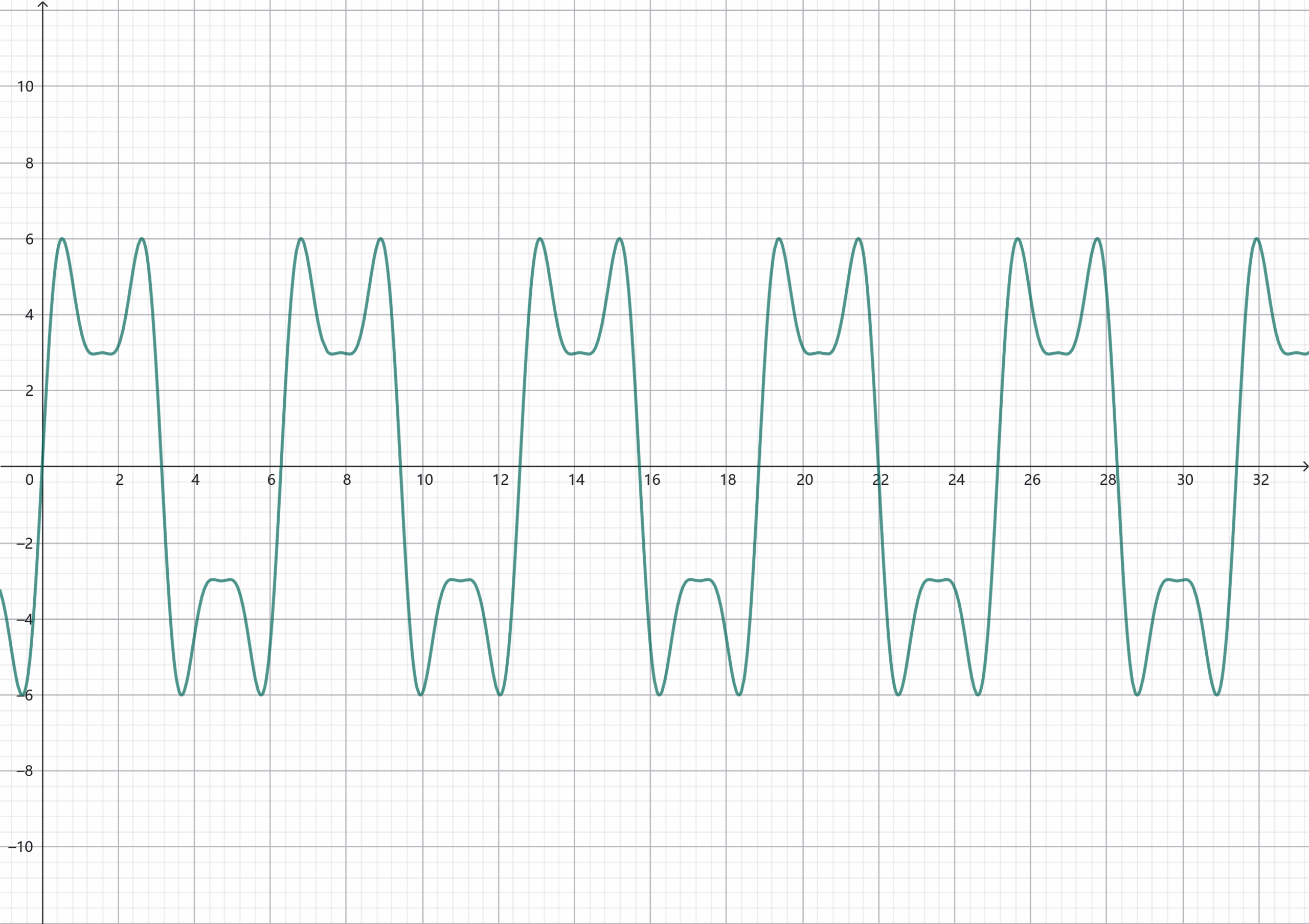
假设横轴是时间，纵轴是信号的幅度，我们先把这个信号的公式写出来：

\(u(t)=sin5t+3sin3t+5sint\)

我们可以发现这个信号全都是由三角函数构成的，而且这些三角函数的周期与幅度都不相同，那么我们是不是可以反过来，来将一个周期信号来用一堆周期与幅度都不同的三角函数来拟合出来，甚至可以更进一步，来把不是周期信号的信号重复无数次让它变成一个周期信号（周期延拓），如果你学过高等数学的话，你知道我们在做什么事情了，这就是傅里叶分解，实际上，只要信号满足一定的条件，我们就可以对它做这种事情，那么问题来了，这关我们要研究的副镜遮挡和鱼骨板什么事情。

在研究傅里叶分解之前，我们必须明确一个问题，傅里叶分解，是将一个（周期）函数分解成一堆的正弦波的方法，但是我们还需要考虑一个问题，就是正弦波的相位问题。实际上的傅里叶分解，我们更多称为傅里叶变换，它将一个复信号变换为一组有含义的复数, 我们利用复数的性质，将相位也包含在了傅里叶变换中，要是想要深入研究它，可以参考关于复变函数与积分变换相关的教材。

二维傅里叶变换

我们之前说的信号是一个关于时间的信号，但是其实傅里叶分解没有说一定是要对时间进行分解，实际上傅里叶分解是一种数学方法，只要你是一个函数，符合傅里叶分解的条件，那么我们就可以对它进行分解。

对于光学来说，我们关注的物体的成像，用比较专业的术语来说就是物平面与像平面之间的关系，既然是平面，显然要用二维的函数来研究它，假设我们成像的波长只有一个，那么成像就变成了一种从物平面到像平面的一种变换，而从物平面到成像元件时的光束长什么样子就决定了最终能够成的像长什么样子，我们既然在研究望远镜，那就直接假设传过来的光是平行光，并且平行光轴入射。那么被遮挡的部分与不被遮挡的部分就构成了一个二值化的函数：

\(u(x,y)=\begin{cases}1, &光能透过去的部分\\ 0, &光透不过去的部分\end{cases}\)

我们来在Python里面利用numpy和matplotlib来绘制一个圆形的二值化函数

它表示了一个口径是1000个单位的无遮挡的望远镜的平行入射光线，我们把它叫做望远镜的孔径函数，这个函数表示望远镜在半径为500个单位以内能够透光，其他部分不透光，那么它对平行光的成像长什么样子呢？其实我们只需要对它进行二维傅里叶变换就可以知道了。

为什么傅里叶变换会展示出像空间，这里就不再深入研究了，感兴趣的话可以去参考一些信息光学的教材或者百科。

好怪呀，正常望远镜的成像不应该是一个艾里斑吗。我们来仔细看看这幅图像的含义，我们假设在图像中点建立一个xy坐标系，那么我们对照之前的傅里叶变换，这幅图里面应该包含孔径函数的各各频率分量的幅度，在这幅图上也就是亮度（与天文摄影时的图像类似，这张图我也进行了非线性拉伸，不然一片黑）。那么问题就在与这幅图上每个点的坐标有什么含义了。

从这幅图来看，中心点是最亮的，然后向周围慢慢的衰减，跟艾里斑一样，但是其中还有相当多的像摩尔纹一样的东西，那我们来改变一下图片来做做实验，就可以搞清楚每个点坐标的含义了。

我们可以发现右图的傅里叶变换出现了一条非常明显的竖线，而对于左图来说，有一个竖直向下的空间频率，也就是说横着的空间频率对应着横线，竖着的空间频率对应着竖线，如果你手头有鱼骨板的话，看看你的鱼骨板长啥样

那我们对它做二维傅里叶变换会变成什么样子呢？

这看起来是不是有点像对上焦点的时候，用鱼骨板出现的3条亮线了吧。

解释到这里，我们可以看到我们并没有去考虑波动光学中每一条光线与其他光线的作用，而是通过傅里叶变换的方法对光线进行分析，粗略的解释了鱼骨板合焦时的图像，实际上，信息光学就是以二维傅里叶变换为基础的研究成像的一门科学，二维傅里叶变换几乎是信息光学的核心。但是，我们仍然留下了很多的问题，比如为什么这几张使用Python的仿真会留下很多奇怪的“残影”，副镜遮挡是怎么影响我们进行拍摄时的分辨力的等等，这需要我们对傅里叶变换有着更深的理解，并且会引入一个信息学中很重要的定理，也就是奈奎斯特采样定理。

奈奎斯特采样定理

准确解释奈奎斯特采样定理是一件艰巨的任务，但是我们还是可以通过一些简单的图像来粗略理解一下这个定理，首先我们就要搞清楚采样是什么意思。

采样

我们在电脑上处理的天文图像，或者是传感器在镜筒上采集到的温度信息都是被量化的，或者叫数字的，一般会按照某种数据格式被计算机或者说数字电路存储和处理，比如如果你学过编程的话就知道有各种int型，float32, float64这样的数据类型。但是实际上真实的世界中存在的数据几乎总是连续的，你的传感器测量出了现在镜筒的温度是10摄氏度，但是可能实际上是10.0235253242345…度，从真实世界上采集数据的过程我们就叫做采样，而采样是通过一个叫做模拟数字转换器（ADC, analog to digital converter）来实现的，它在采样的过程中，将一个电压（我们几乎总是将各个物理量转化成电压）转化成计算机所理解的二进制数，它转化出的二进制数按照某种协议被计算机处理成我们能理解的单位，比如10摄氏度，我们在查看天文相机的时候往往会看到ADC位数，比如常见的IMX715会转化成12bit, IMX571是16bit, 这个位数就是CMOS中内置的ADC将采集到的电压转化为数字时的位数。

比如一个ADC能对0V到1V的电压转化为12bit二进制数，那么它就能将1V这个范围的电压分划出4096个值，而对于16bit的ADC就是65536个，所以一般来说位数越高，采样下来的图像越不容易出现色阶断层之类的问题。

但是除了采样精度，ADC在采样的时候还有一个关键的问题，那就是ADC在将模拟量（即真实世界中的量）转化为数字量的时候，会消耗一定的时间，比如对一个正弦波：

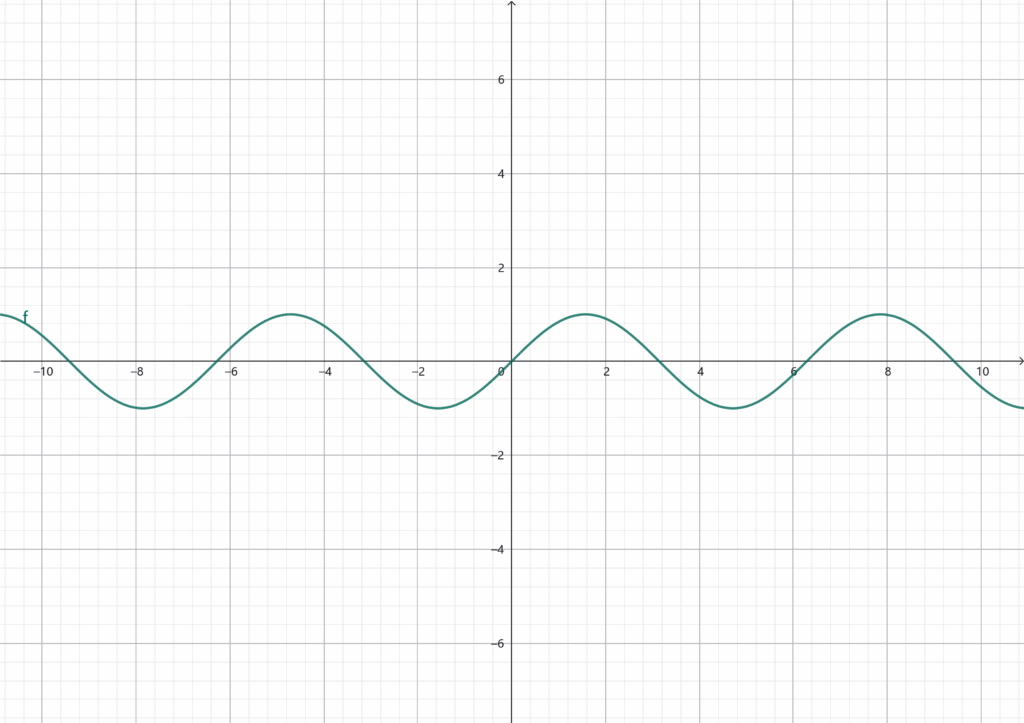
我们可能只能采集到一些离散的点，比如我们假设每隔0.5采样一个点

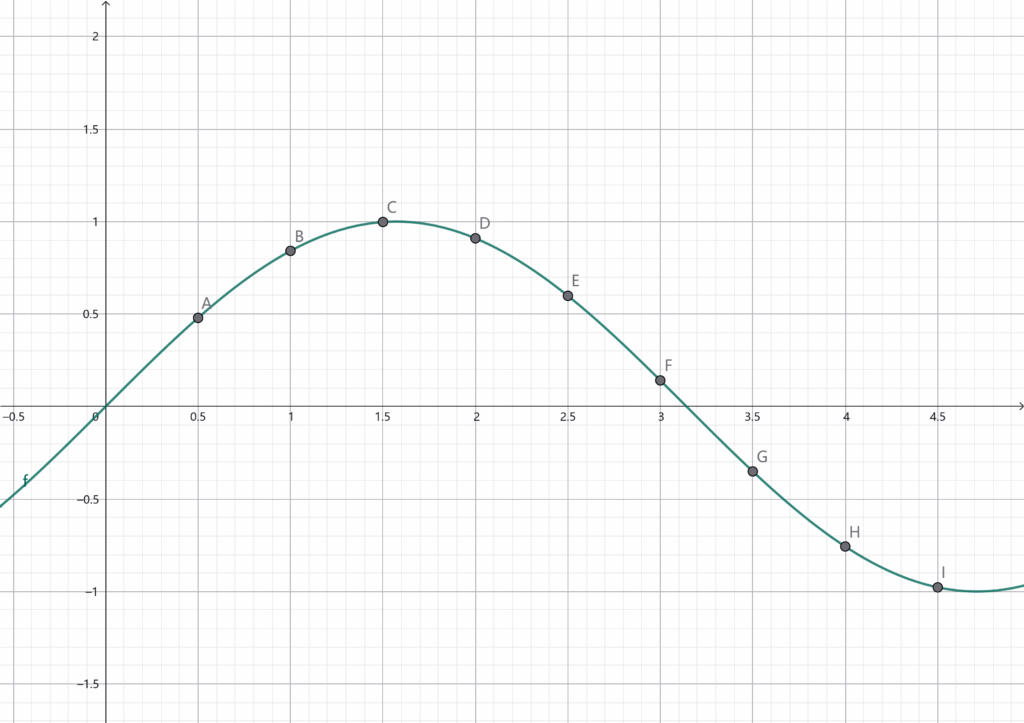
这时候我们能看到的就只剩下这些点了，图中的绿色函数是真实世界中的，但是在数字系统中并不存在，那我们拿着一堆点这么能确定我们采样得到的函数原来长什么样子呢？如果我们采样的够密，那就无所谓了，但是，这样会消耗很多的资源，尤其对于ADC来说，采样间隔的缩短会让ADC的价格翻一翻，那有没有什么方法能够确定我们正好需要的采样间隔呢？

采样率与采样定理

从直观上来看，如果信号变化的速度很慢，那么相应的我们的采样间隔就可以很大，如果用数学一点的语言来看的话，信号变化的速度就对应到信号的频率，采样间隔我们也可以等效成采样频率，采样频率有：

\(f_{采样}=\frac{1}{t_{采样间隔}}\)

那么信号的频率是什么呢，傅里叶变换！傅里叶变换将信号中存在的各个频率分量拆分了出来，假如一段信号中含有0到500Hz的频率，那么我们需要的采样频率是多少呢，奈奎斯特指出了需要的最低采样频率是信号中含有的最高频率的两倍，也就是1000Hz, 这就是奈奎斯特采样定理。至于这个定理的证明过程，需要涉及一些复杂的数学知识，所以我们就又又又从略了。

混叠现象

奈奎斯特采样定理告诉了我们采样频率的下限，那如果我非要违背这个定理会发生什么事情呢？

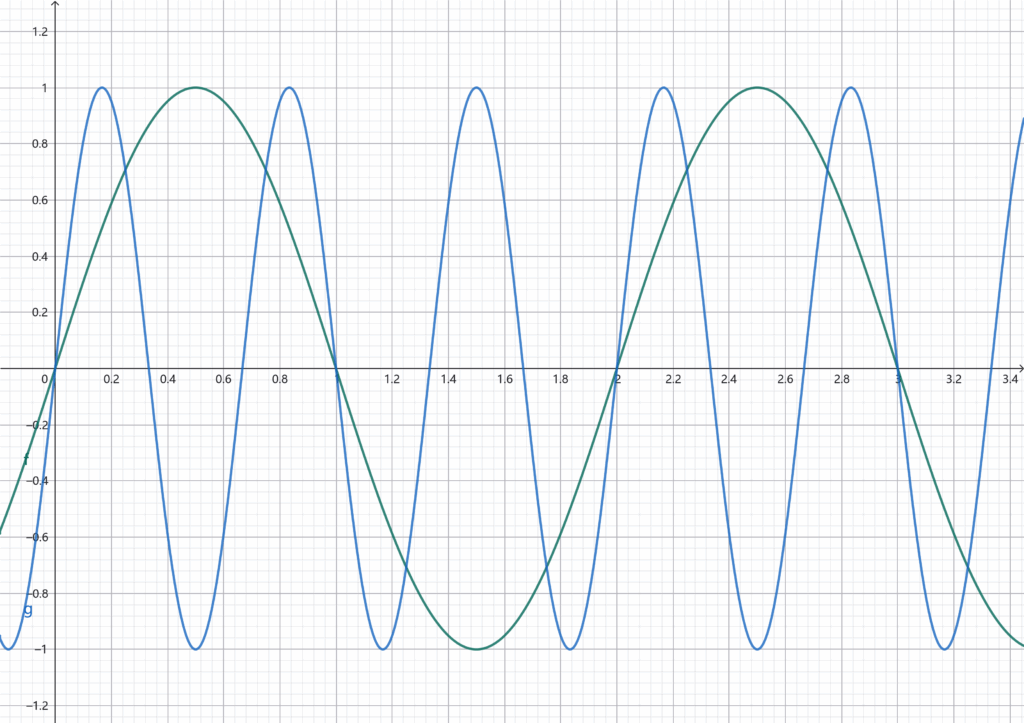
仔细观察这两个函数图像，尤其是它们两个的交点位置，你会发现这两个图像的交点同样会有周期性，假如我们采样得到的点就是这些交点，请问我们采样的原始信号是蓝色的信号还是绿色的信号呢？换一句话来说，假如我们向一个ADC中通入这两个信号，而ADC的采样间隔过大，那么它是分辨不了这两个信号的，如果我们对ADC采样得到的信号做傅里叶变换的话，尽管我们通入的信号是蓝色的，但是在频谱图上面我们会发现绿色函数图像对应的频率。

下面我们用仿真工具来实验一下吧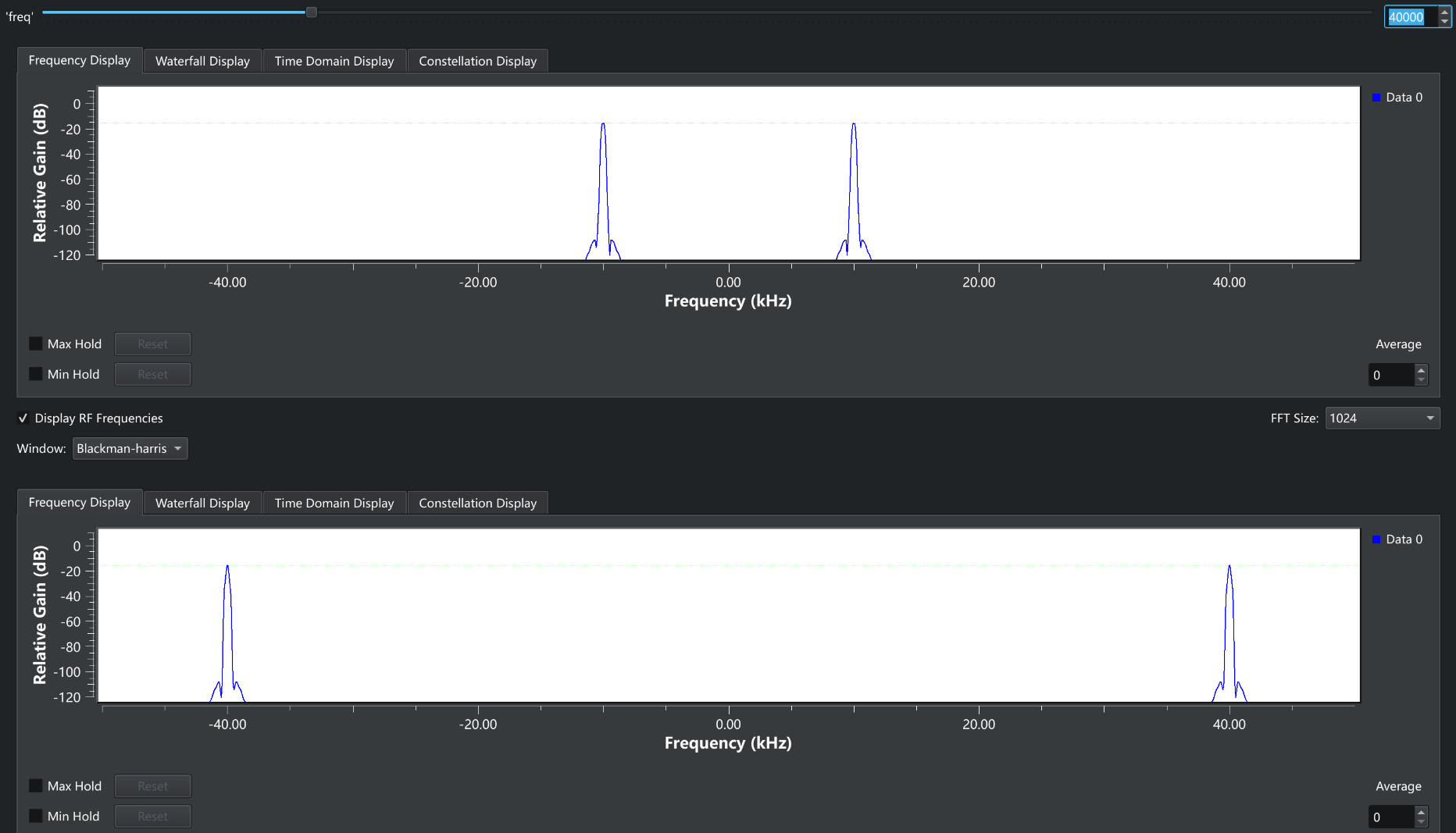

右上角就是我们输入的频率，下面两个窗口就是对应的频谱图，负数频率是傅里叶变换在复数域中形成的，我们不去管它就可以了上面那个窗口是10kHz的参考频率，下面的则是输入的频率，现在是40kHz, 可以看到现在的频谱图显示出来了正确的频率，现在我们来增大输入频率。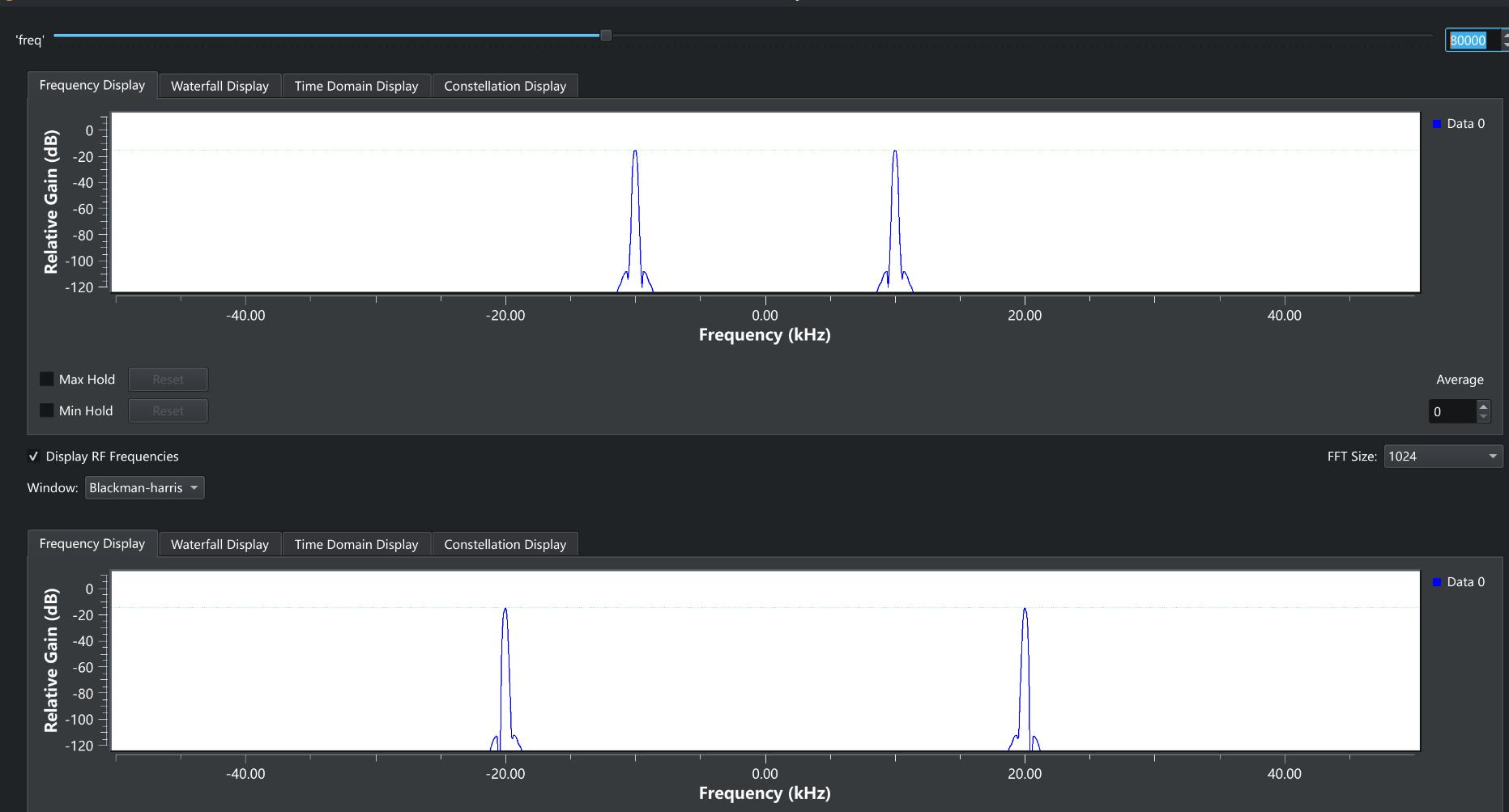

现在输入的频率是80kHz,但是我们发现频谱图上的频率却变成了20kHz, 现在的采样频率是100kHz, 如果我们将80kHz也画在频谱图上面的话，你就会发现两边的频率是关于采样频率的二分之一是对称的，如果你想象一下频率慢慢增大，那么那个低频率的峰就会慢慢向右边移动，撞上50kHz的“墙”，然后被反射回来一样。

铺垫到这里，我们研究的是不是又回到了时间域上，那么空间域上的二维傅里叶变换是不是也一样呢，现在我们来再看看鱼骨板的二维傅里叶变换图

图像中的三条线是不是像从中心出发，射向周围，碰到了“墙”被反射，然后又碰到了“墙”被反射的样子，这就说明了采样间隔不够啊，时间上的采样间隔是ADC两次采样之间的时间，那空间上的采样间隔相应的是什么呢？

当然是传感器的像素密度了，这幅鱼骨板图像是计算机生成的，并不够细腻，所以出现了这种混叠的现象，在正常使用中，鱼骨板的图像是不会出现这种情况的，因为傅里叶变换是在自然的情况下，从鱼骨板对望远镜的遮挡到CMOS的成像面的过程自然完成了傅里叶变换，所以我们在对焦的时候几乎不会发生这种情况。

仿真的问题

解决了混叠的问题，我们还有一些其他的问题，比如对一个圆形的孔径函数，为什么进行傅里叶变换后不是一个艾里斑呢？

这个问题本质上与鱼骨板问题一样，都是计算机对真实世界不完美的近似，在圆形的孔径函数那幅图中，我们生成的圆形并不是圆形，它总归是像素的拟合，如果我们用更加精细的图像，应该会取得更好的效果。

是不是比之前要精细多了呢。（这个图片原图有TM 150多MB的大小，现在是被jpg压缩后只剩下4MB的大小了，中间的光斑来自于被过分压缩的jpg算法，jpg算法的本质之一就是对图片的高频部分进行了压缩。）

未完待续…

科普信息光学是一个大工程，写这篇文章的本意是想解释一下跟鱼骨板想关的问题，但是实际上信息光学跟我们的天文摄影处处相关，所以不出意外的写的超长了，所以先写到这里吧，我们来列一下还没有解决的问题

1. 鱼骨板没合焦时候为什么要长那个样子
2. 遮挡是怎么影响分辨力的

这两个问题背后又会是这样一篇超长的文章了看来。

坑还是不能随便挖的呀。